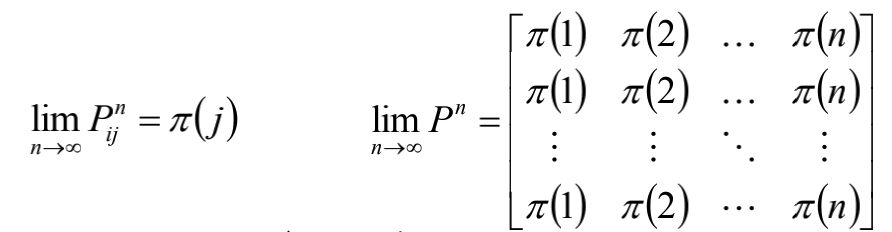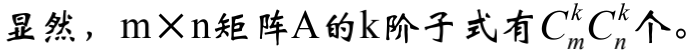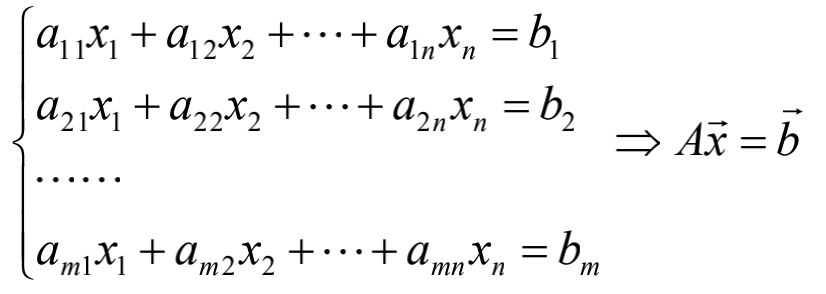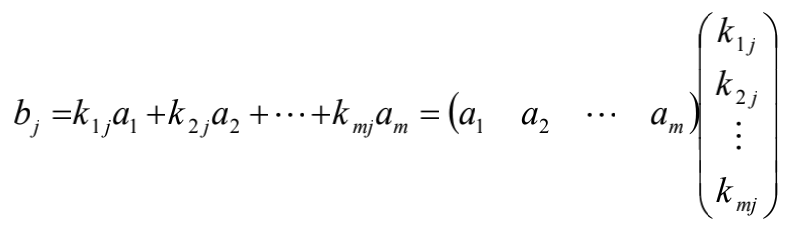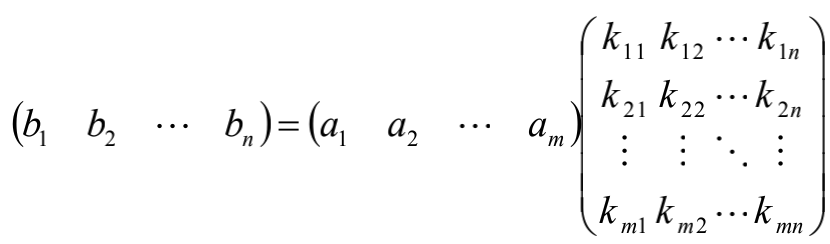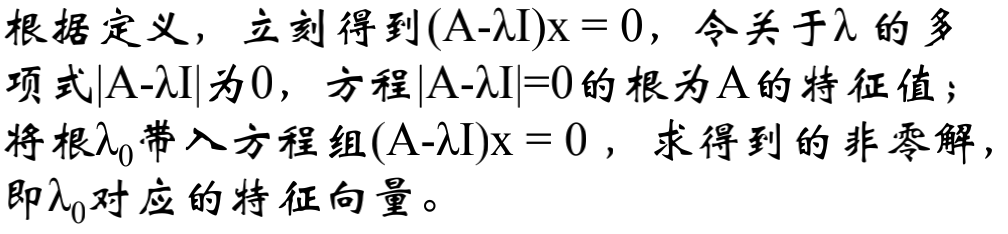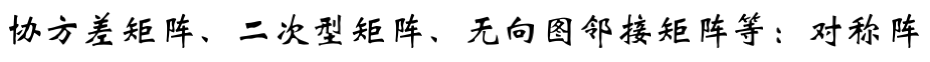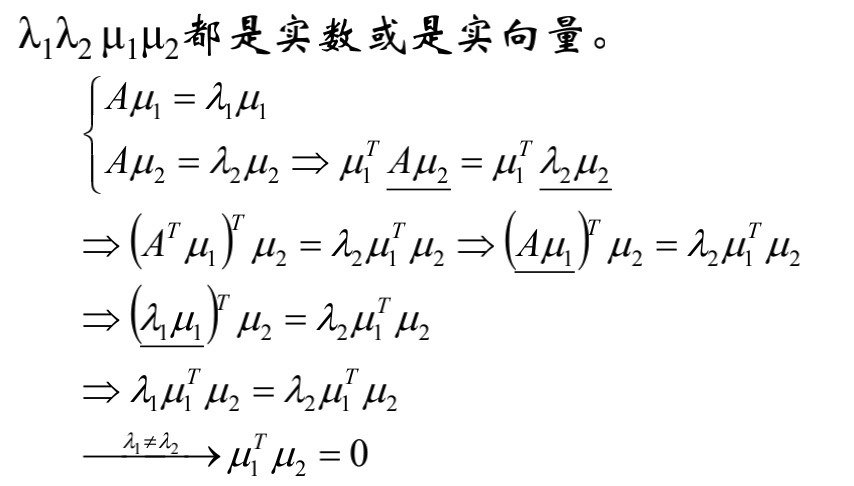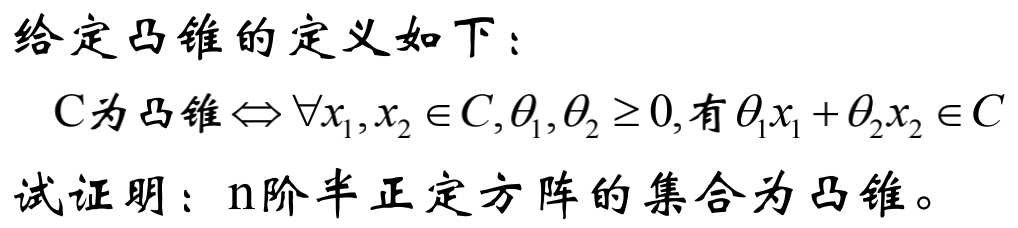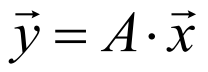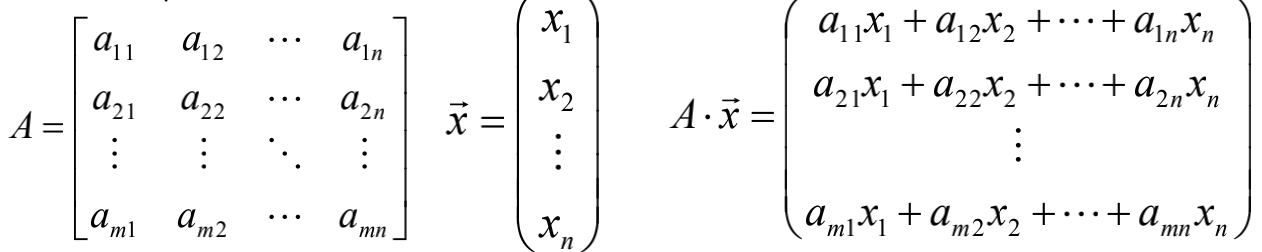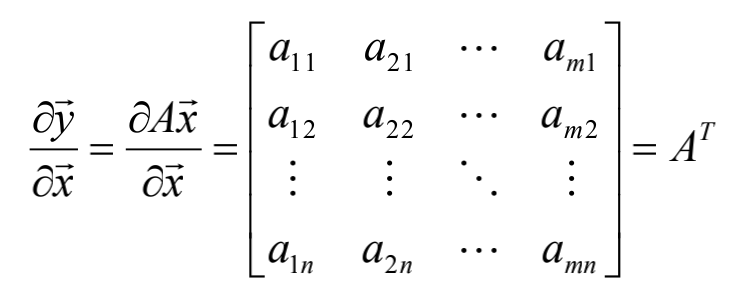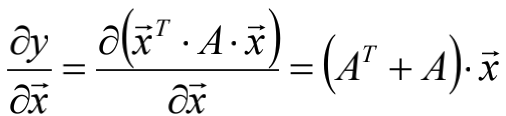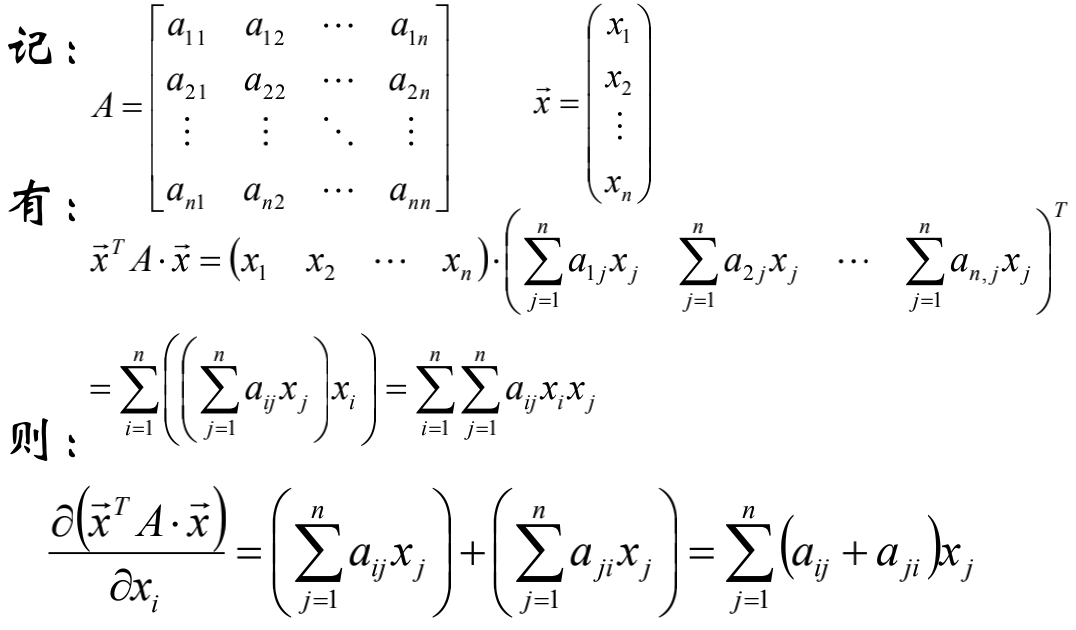主要内容
矩阵
SVD的提法
(AT⋅A)vi=λivi⇒⎩⎪⎪⎨⎪⎪⎧σi=λiui=σi1A⋅νi⇒A=UΣVT
- 奇异值分解(Singular Value Decomposition)是一种重要的矩阵分解方法,可以看做对称方阵在任意矩阵上的推广。
- 假设A是一个m×n阶实矩阵,则存在一个分解使得:
Am×n=Um×mΣm×nVn×nT
通常将奇异值从大到小排列,这样∑就能由A唯一确定了。
与特征值、特征向量的概念相对应
*∑在对角线上的元素称为矩阵A的奇异值;
- U的第i列称为A的关于σi的左奇异向量;
- V的第i列称为A的关于σi的右奇异向量。
例子:
己知4x5阶实矩阵A,求A的SVD分解:
A=⎣⎢⎢⎢⎡10000004030000002000⎦⎥⎥⎥⎤
U=⎣⎢⎢⎢⎡0001010010000010⎦⎥⎥⎥⎤
Σ=⎣⎢⎢⎢⎡40000300005000000000⎦⎥⎥⎥⎤
VT=⎣⎢⎢⎢⎢⎢⎡000.200.8100000100000010000.80−0.2⎦⎥⎥⎥⎥⎥⎤
矩阵U和V都是单位正交方阵:UTU=I, VTV=I
线性代数
方阵的行列式
- 一阶方阵的行列式为该元素本身
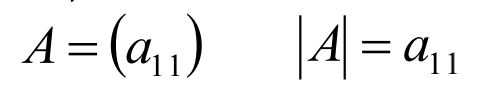
- n阶方阵的行列式等于它的任意行(或列)的各元素与其对应的代数余子式乘积之和
*2×2的方阵
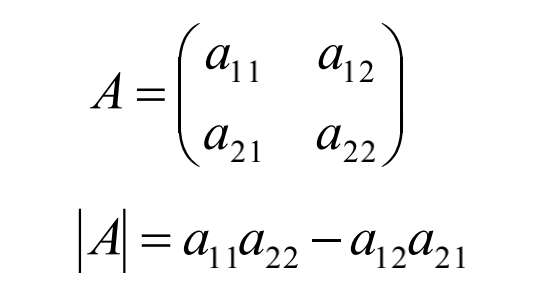
代数余子式
在n阶行列式D中划去任意选定的k行、k列后,余下的元素按原来顺序组成的n-k阶行列式M,称为行列式D的k阶子式A的余子式。如果k阶子式A在行列式D中的行和列的标号分别为i1,i2,…,ik和j1,j2,…,jk。则在A的余子式M前面添加符号:
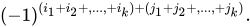
后,所得到的n-k阶行列式,称为行列式D的k阶子式A的代数余子式。
伴随矩阵
对于n×n方阵的任意元素aij都有各自的代数余子式Aij=(−1)i+jMij,构造n×n的方阵A^\*;
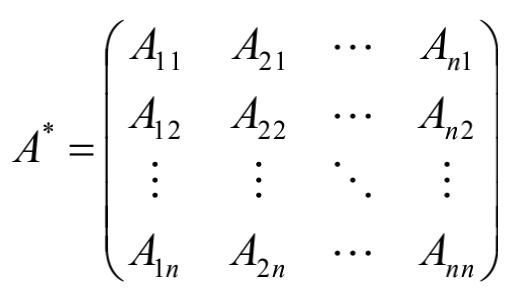
A^_称为A的伴随矩阵。注意,Aij位于A_的第j行第i列。
方阵的逆
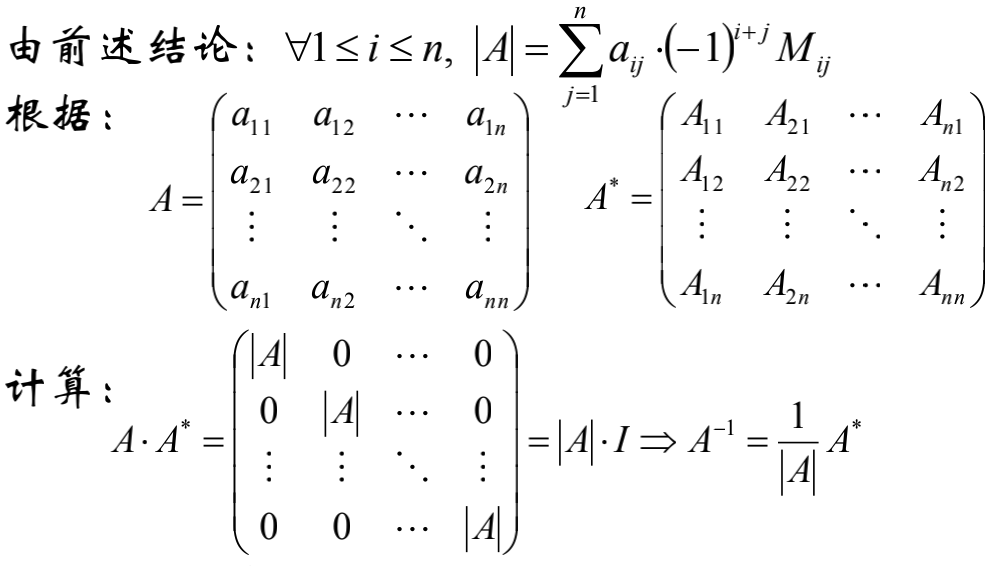
范德蒙行列式Vandermonde
范德蒙行列式:

第n行是x1,x2,...,xn的n-1次幂。
如果我们能使得x1,x2,...,xn互不相等,那么矩阵D不为0,则存在D−1
矩阵的乘法
A为m×s阶矩阵,B为s×n阶的矩阵,那么,C=A×B是m×n阶的矩阵,其中:
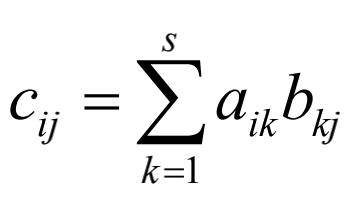
矩阵模型
考虑随机过程i,它的状态有n个,用1~n表示。记在当前时刻t时刻时位于i状态,它在t+1时刻处于j状态的概率为P(i,j)=P(ji)。
即状态转移的概率只依赖于前一个状态
(思考马尔可夫过程?)

举例:
假定按照经济状况将人群分为上中下三个阶层,用123表示。假定当前处于某阶层只和上一代有关,即,考察父代为第i阶层,则子代为第j阶层的概率。假定为如下转移概率矩阵:

图解为:
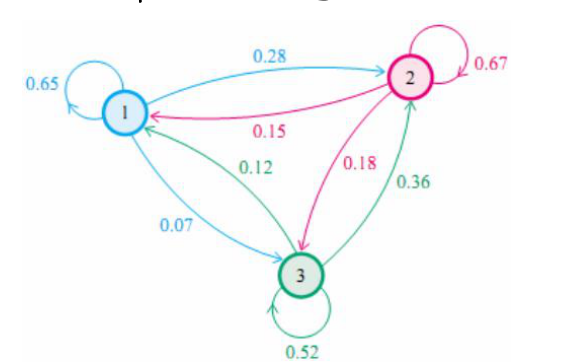
概率转移矩阵
第n+1代处于第j个阶层的概率为:
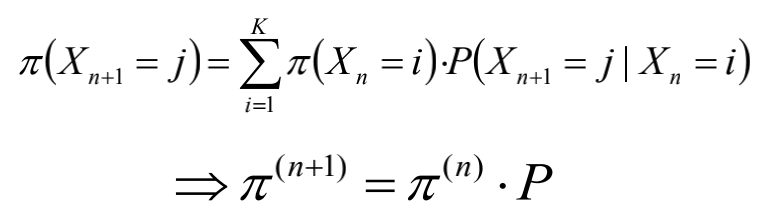
矩阵P即为(条件)概率转移矩阵。
第i行元素表示,在上一状态为i时的分布概率,每一行元素的和为1.
那么思考:初始概率分布对最终分布的影响?
Think!
初始概率i =\[0.21,0.68,0.1\]迭代
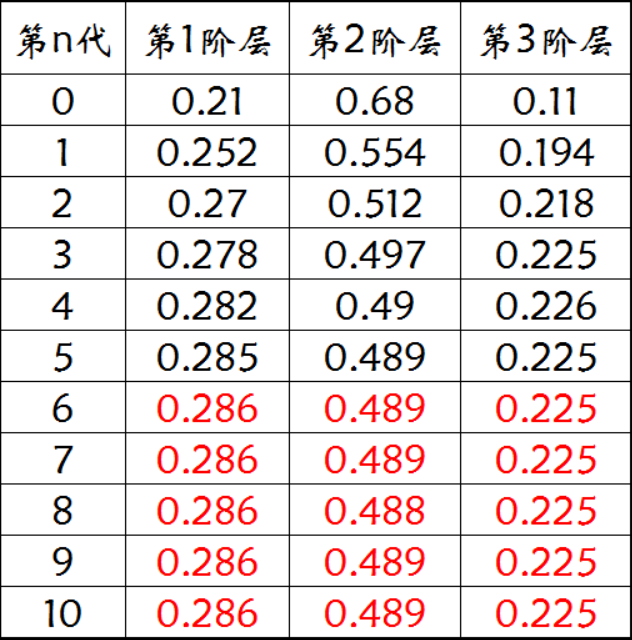
初始概率i =\[0.75,0.15,0.1\]迭代
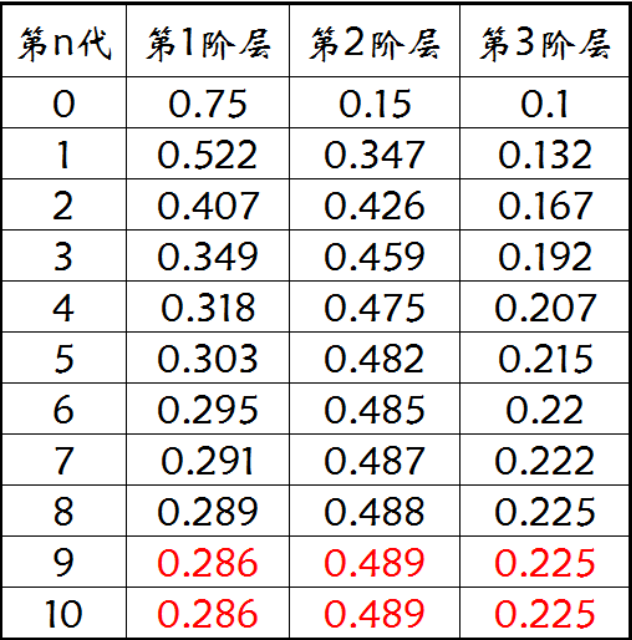
平稳分布
初始概率不同,但经过若干次迭代,i最终稳定收敛在某个分布上。这是转移概率矩阵P的性质,而非初始分布的性质。
上例中,矩阵P的n次幂,每行都是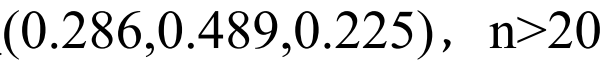 ,这实际上就是特征向量。
,这实际上就是特征向量。
如果一个非周期马尔可夫随机过程具有转移概率矩阵P,且它的任意两个状态都是连通的,则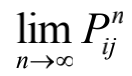 存在,记作
存在,记作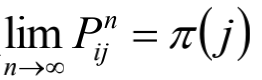 。
。
In Fect,下面两种写法等价:
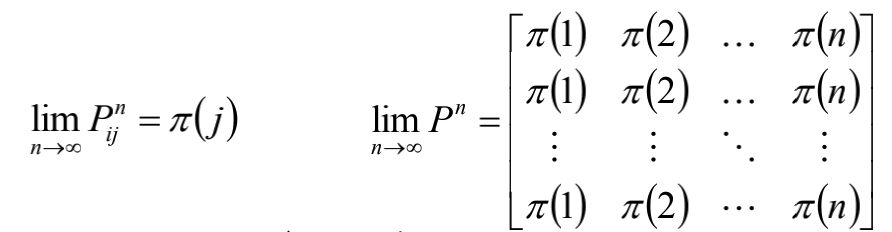
同时,若某概率分布iP=i,说明
矩阵和向量的乘法

矩阵和向量的乘法应用
矩阵的秩
在m×n矩阵A中,任取k行k列,不改变这k2个元素在A中的次序,得到k阶方阵,称为矩阵A的k阶子式。
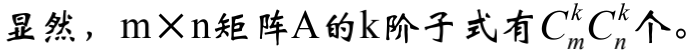
设在矩阵A中有一个不等于0的r阶子式D,且所有r+1阶子式(如果存在)全等于0,那么,D称为A的最高阶非零子式,r称为A的秩,记作R(A)=r

秩与线性方程组解的关系
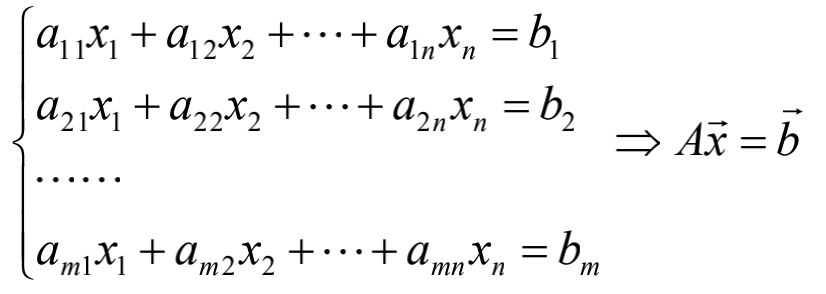

推论
- Ax=0有非零解的充要条件是R(A)<n
- Ax=b有解的充要条件是R(A)=R(A,b)
向量组等价

系数矩阵
将向量组A,B所构成的矩阵依次记作A(a1,a2,...,am)和B(b1,b2,...,bm),B组能由A组线性表示,即对于每个向量bi,存在k1j,k2j,...,kmj
使得:
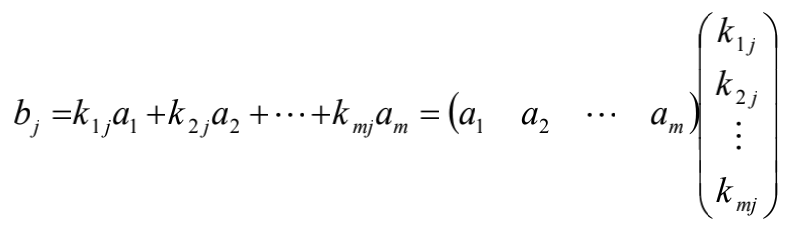
从而得到系数矩阵K
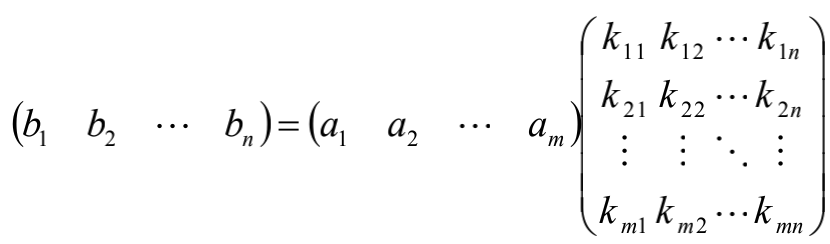
对C=AB的重新认识
由上,若C=A×B,则矩阵C的列向量由A的列向量线性表示,B即为这一表示的系数矩阵;C同样由B的行向量线性表示,A为这一表示的系数矩阵。
向量组B:b1,b2,...,bn能由向量组A:a1,a2,...,an线性表示的充要条件是矩阵A=(a1,a2,...,an)的秩等于矩阵(A,B)=(a1,a2,...,an,b1,b2,...,bn)的秩。
正交阵
若n阶矩阵A满足ATA=I,称A为正交矩阵,简称正交阵。
I为对角线为1,其他为0的矩阵
A是正交阵,x为向量,则Ax称作正交变换。
正交变换不改变向量长度。
特征值和特征向量
A是n阶矩阵,若数λ和n纬非0列向量x满足Ax=λx,那么数λ称为A的特征值,x称为对应于特征值的特征向量。
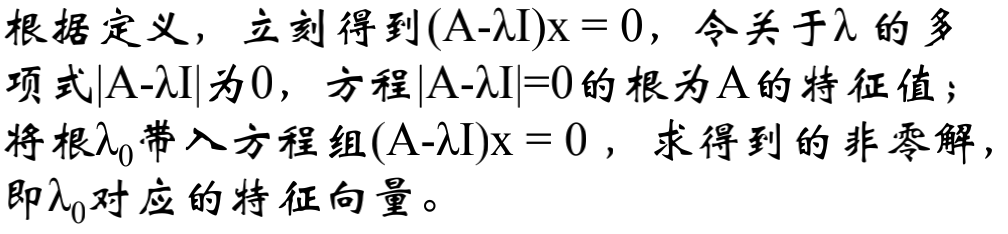
特征值的性质
设n阶矩阵A(aij)的特征值为λ1,λ2,...,λn,则:
λ1+λ2+...+λn=a11+a22+...+ann
λ1λ2...λn=A
矩阵A主对角线行列式的元素和,称作矩阵A的迹
不同特征值对应的特征向量

- 不同特征值对应的特征向量,线性无关。
- 若方阵A是对称阵,结论是否加强?
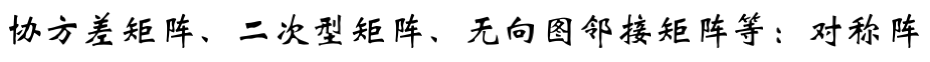
引理
实对称阵的特征值是实数

应用:
将实数λ带入方程组(A−λI)x=0,该方程组为实系数方程组,因此,实对称阵的特征向量可以取实向量。
实对称阵的不同特征值的特征向量正交
令实对称阵为A,其两个不同的特征值λ1λ2对应的特征向量分别是μ1μ2;
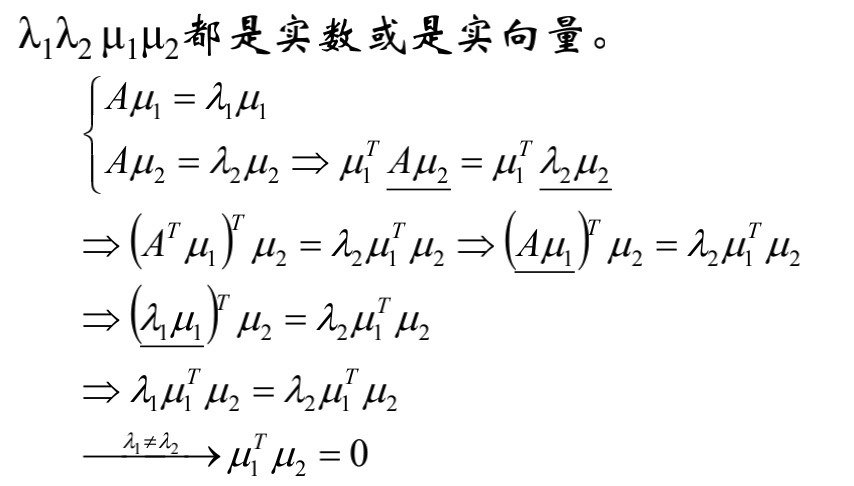
最终结论

正定阵
对于n阶方阵A,若任意n阶向量x,都有x^TAx>0则称A是正定阵。
若条件变为xTAx≥0,则A称作半正定阵。
类似的还有负定阵,半负定阵。
给定任意m×n的矩阵A,证明ATA一定是半正定阵。
正定阵的判定
- 对称阵A为正定阵;
- A的特征值都为正;
- A的顺序主子式大于0;
- 以上三个命题等价。
例题:
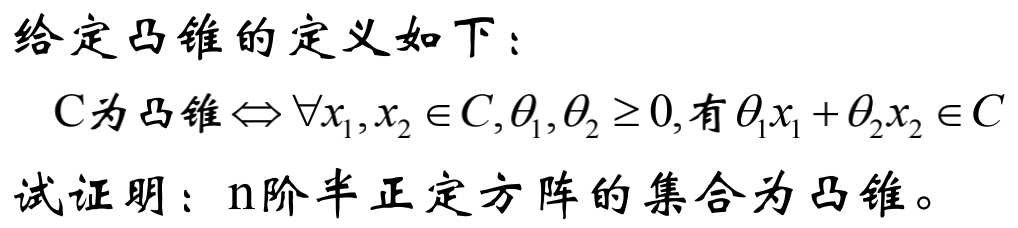
定义证明:

向量的导数
A为m×n的矩阵,x为n×1的列向量,则Ax为m×1的列向量,记为:
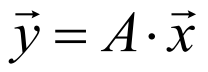
推导
令:
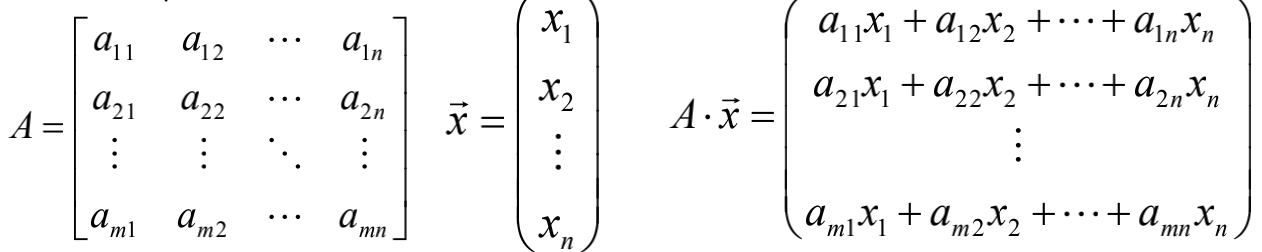
从而:
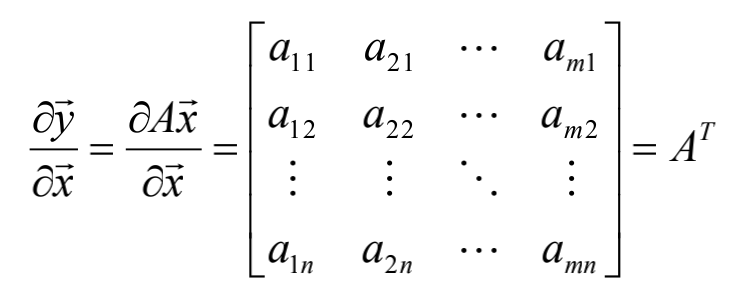
结论与直接推广

注意
关于列向量求导,资料中有如下方案:
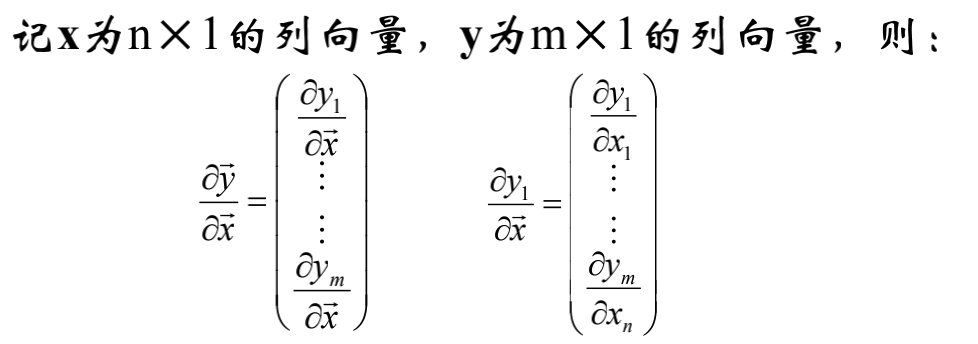
以上公式将会导致向量间求导得到“超越矩阵”-矩阵的每个元素仍然是一个矩阵,不利于应用。
标量对向量的导数
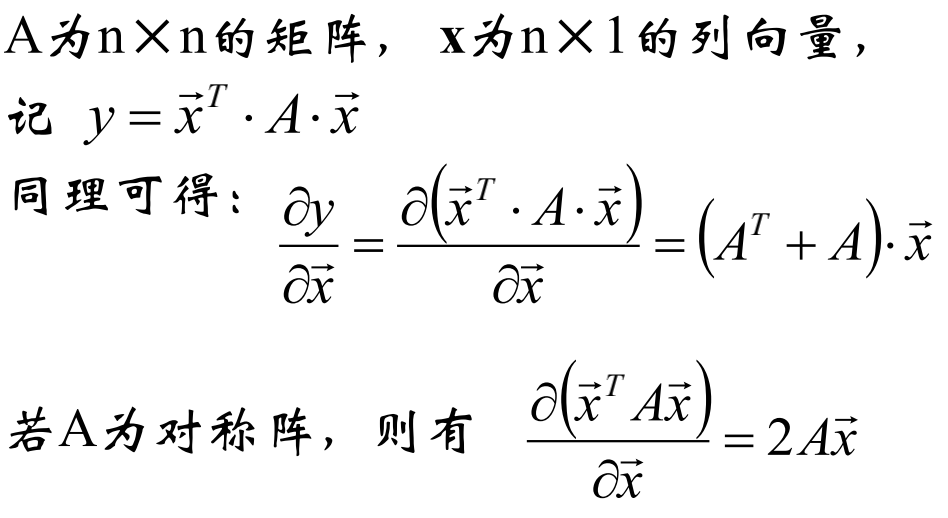
推导公式: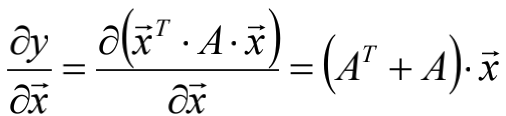
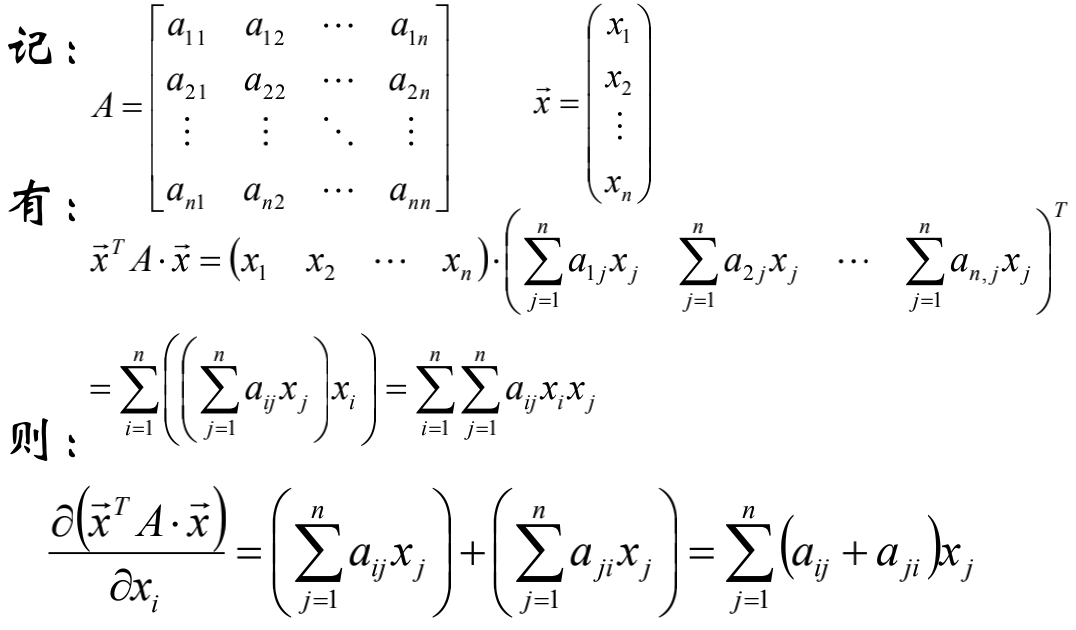
标量对方阵的导数

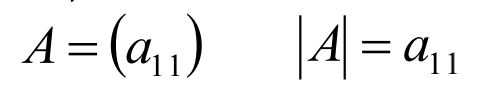
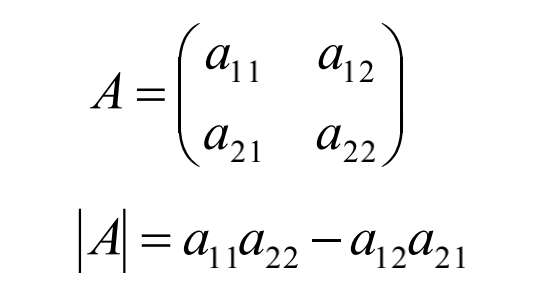
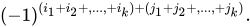
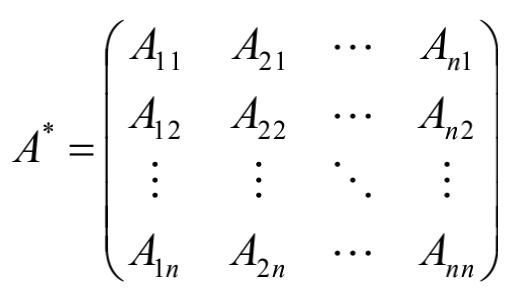
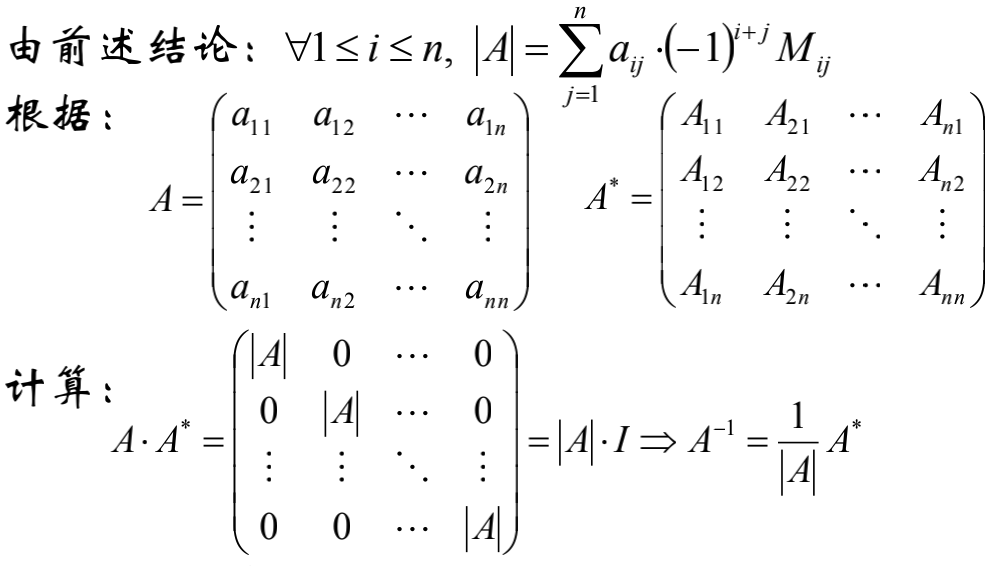

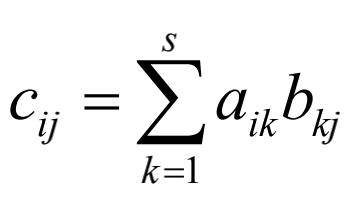



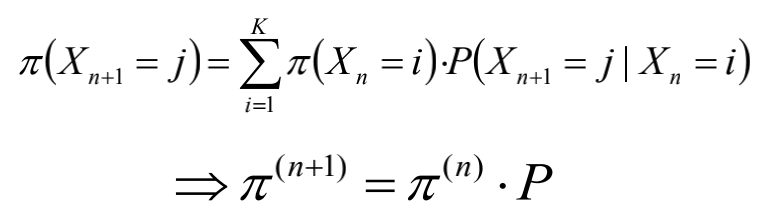


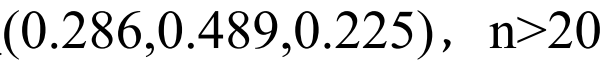 ,这实际上就是特征向量。
,这实际上就是特征向量。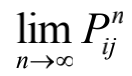 存在,记作
存在,记作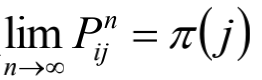 。
。